例題: 累乗を求める

Scratch（スクラッチ）で累乗を求めるプログラムを作成してみます。 「3の2乗 = 9」みたいな計算です。 べき乗（冪乗）と言われることもありますが、べき乗は指数が自然数ではない場合も含むので、ここでは指数が自然数の場合のみを考え、累乗と呼ぶことにします。

シンプルに繰り返す累乗計算

Scratch（スクラッチ）には今のところ累乗を計算する演算ブロックが無いので、必要なら自力で計算することになります。 シンプルに「aのn乗」を求めるにはaをn回かけ合わせれば良いです。

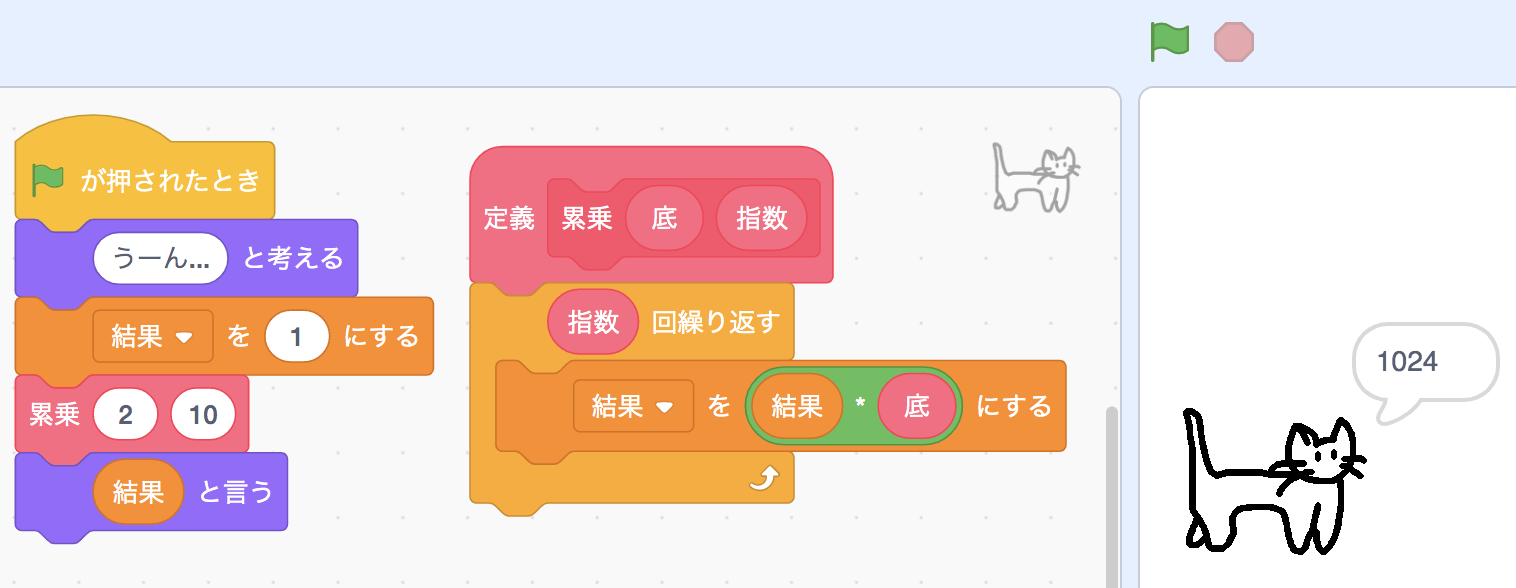
累乗の計算は複数箇所で使う可能性があるので、再利用性を高めるためにブロック定義として切り出すと良いと思います。

バイナリ法による累乗計算の高速化

以下の内容は発展的な内容です。

上に書いた方法で正しく答えは求まっているのですが、あのやり方は遅くないでしょうか。 遅いんですよ。 例えば「2の1億乗を10007で割った余りを求めなさい」みたいな問題があったとします（こういうのは競技プログラミングでよくあります）。 さっきのプログラムでこれを計算すると……

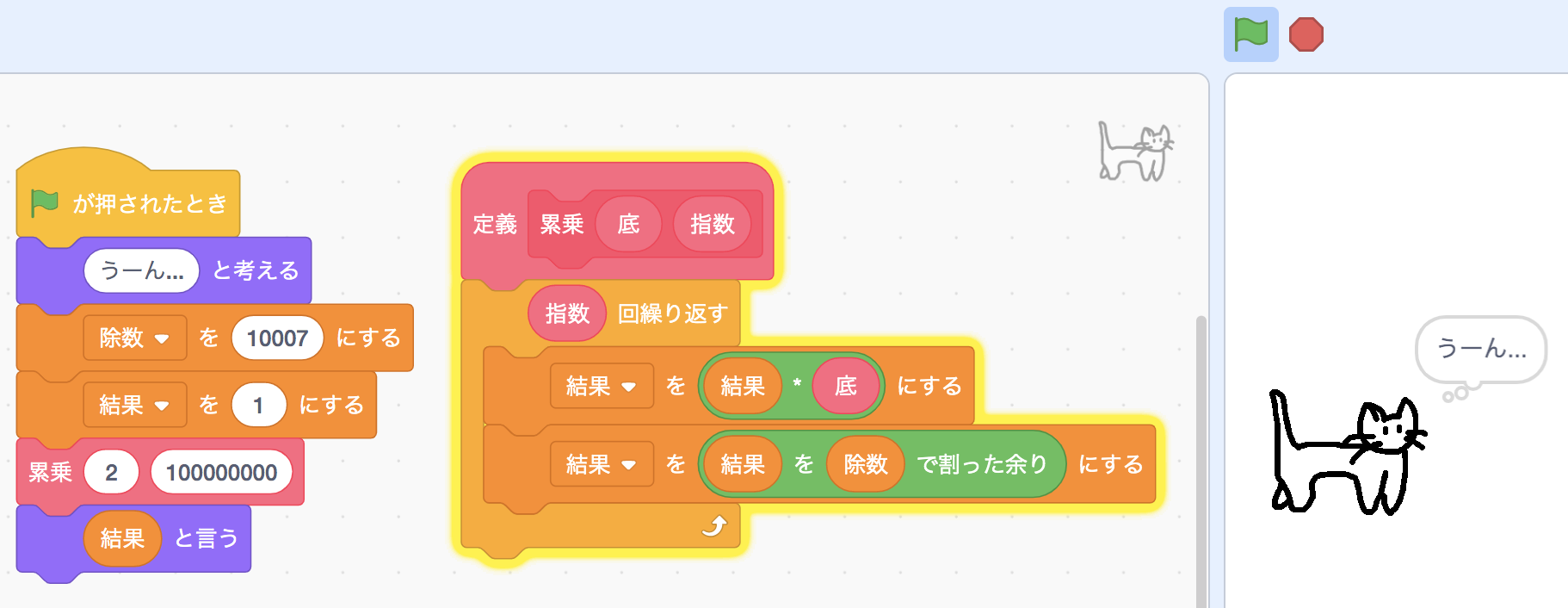
ネコのスプライトが「うーん……」と考えたまま硬直しました。 1億回繰り返す必要があるので処理に時間がかかっているのです。 ちゃんと図ってないですが、100万乗のときに3秒かかったので、1億乗は300秒（5分）くらい放置していれば答えが出ると思います。

数の性質を利用すれば劇的に計算時間を短縮することができます。

• aのn乗は…
  • nが偶数のとき、「aの(n/2)乗」の2乗に等しい
  • nが奇数のとき、「aの((n-1)/2)乗」の2乗 かける a に等しい

この性質を使えば、1億回ループする代わりに、なんと28回の再帰呼び出しで1億乗の値を求めることができ、計算速度が劇的に向上します。

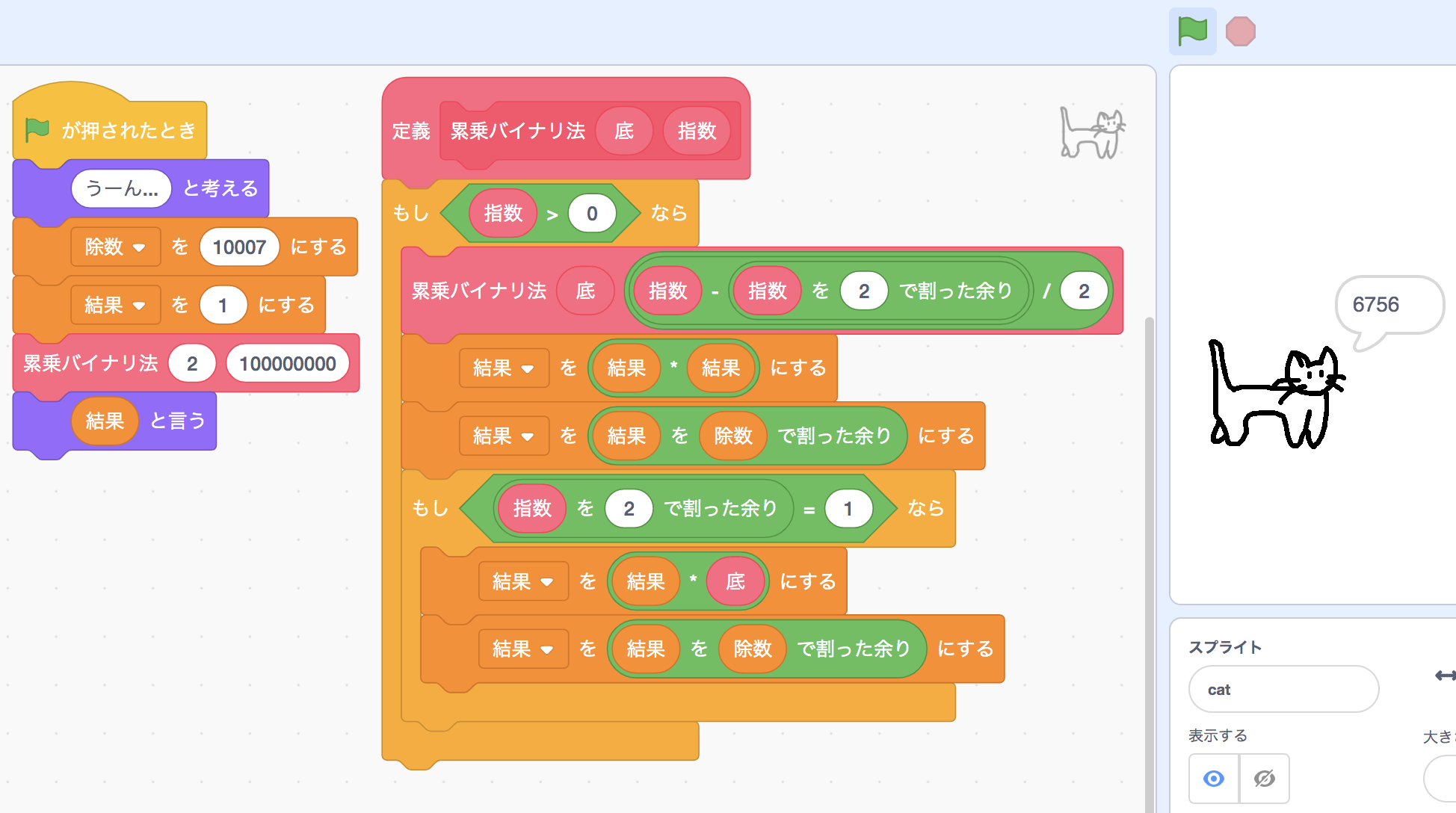
この累乗計算の高速化手法は「バイナリ法」といった名前で呼ばれています。 専門的には「計算量がO(N)からO(logN)に改善した」みたいな言い方をします。

実際の業務でも、こういった計算量の改善でシステムが爆速化するということはたまに起きるので、プログラミングにおいてアルゴリズムの計算量というのは重要な概念です。

Scratchプロジェクト共有を共有しているので良かったら触ってみてください→累乗計算を高速に行うプログラム

おまけ: C++で累乗計算

ここで紹介した累乗計算のScratchプログラムと同等の処理を行うC++のプログラムを掲載します。 眺めてみて「Scratchと同じだなぁ」と思っていただければオッケーです。

#include <iostream>

const int MOD = 10007;

using namespace std;

// シンプルに繰り返す累乗計算
int my_exp(int a, int n) {
  int ret = 1;;
  for (int i = 0; i < n; i++) {
    ret = ret * a;
    ret = ret % MOD;
  }
  return ret;
}

// バイナリ法で高速化した累乗計算
int my_exp_fast(int a, int n) {
  if (n == 0) {
    return 1;
  }
  int ret = my_exp_fast(a, n / 2);
  ret = ret * ret;
  ret = ret % MOD;
  if (n % 2 == 1) {
    ret = ret * a;
    ret = ret % MOD;
  }
  return ret;
}

int main(void) {
  cout << my_exp_fast(2, 100000000) << endl;
  return 0;
}

実行結果

$ ./a.out
6756