プログラミング教育のためのスクラッチ例題集

# 例題: ハノイの塔

再帰的プログラミングの典型的な例題である「ハノイの塔」を解くプログラミングをScratchでやってみましょう。

ハノイの塔は1833年にフランスの数学者エドゥアール・リュカによって考案された数学的なパズルゲームです。 一見すると解くために複雑な処理が必要なように思われるのですが、再帰的プログラミングを知っていると劇的に簡単に処理を書けて感動するので、プログラミングの授業などではよく登場します。

映画「猿の惑星: 創世記」でチンパンジーの知能測定に使われているシーンがあったので、ハノイの塔という名前は知らなくても見たことある方はいらっしゃるかと思います。

下の写真は家にあったハノイの塔の実物です。

ハノイの塔の実物

# ハノイの塔のルール

  • 3本の柱と、N枚の大きさが全て違う円盤がある
  • 最初は一番左の柱に全ての円盤が、大きなものが下になるように刺さっている
  • この円盤を全て一番右の柱に動かせればゲームクリア

ただし円盤の動かし方に次の制限があります。

  • 一度にどれかの柱の一番上の1枚の円盤しか動かせない
  • 円盤は柱以外の場所には置けない
  • ある円盤は、それより小さな円盤の上に置くことはできない

# ハノイの塔の概念的な解き方

3本の柱をA, B, Cと呼ぶことにし、4枚の円盤をAからCに動かしたいとします。 このときの動かし方は次のようになります。

  • 小さい方から3枚をAからBに「何らかの方法」で移動させる
  • 4枚目をAからCに移動させる
  • 小さい方から3枚をBからCに「何らかの方法」で移動させる

ハノイの塔の概念的な解き方

小さい方から3枚の移動ができれば4枚の移動もできるということが分かります。 また小さい方から3枚を移動させる際、それ以外の円盤は全てこの3枚より大きいため地面と同じだと見なすことができます。 よって3段のハノイの塔がクリアできるのであれば、4段のハノイの塔がクリアできます。

一般化して次のことが言えます。

  • k段のハノイの塔がクリアできれば、k+1段のハノイの塔がクリアできる
  • 0段のハノイの塔は「何もしない」という操作によりクリアできる

数学的帰納法により、何段あってもハノイの塔はクリアできるということになります。 またその解法となるk段のハノイの塔の動かし方は、次のように再帰的に定義できます。

  • k=0の時は何もしない
  • そうでなければ
    • 小さい方からk-1枚を出発地から休憩地に動かす
    • 1枚を出発地から目的地に動かす
    • 小さい方からk-1枚を休憩地から目的地に動かす

# Scratchでハノイの塔を解くプログラム

ここまでの内容をScratchのプログラムに落とし込むと、次のようにコーディングできます。

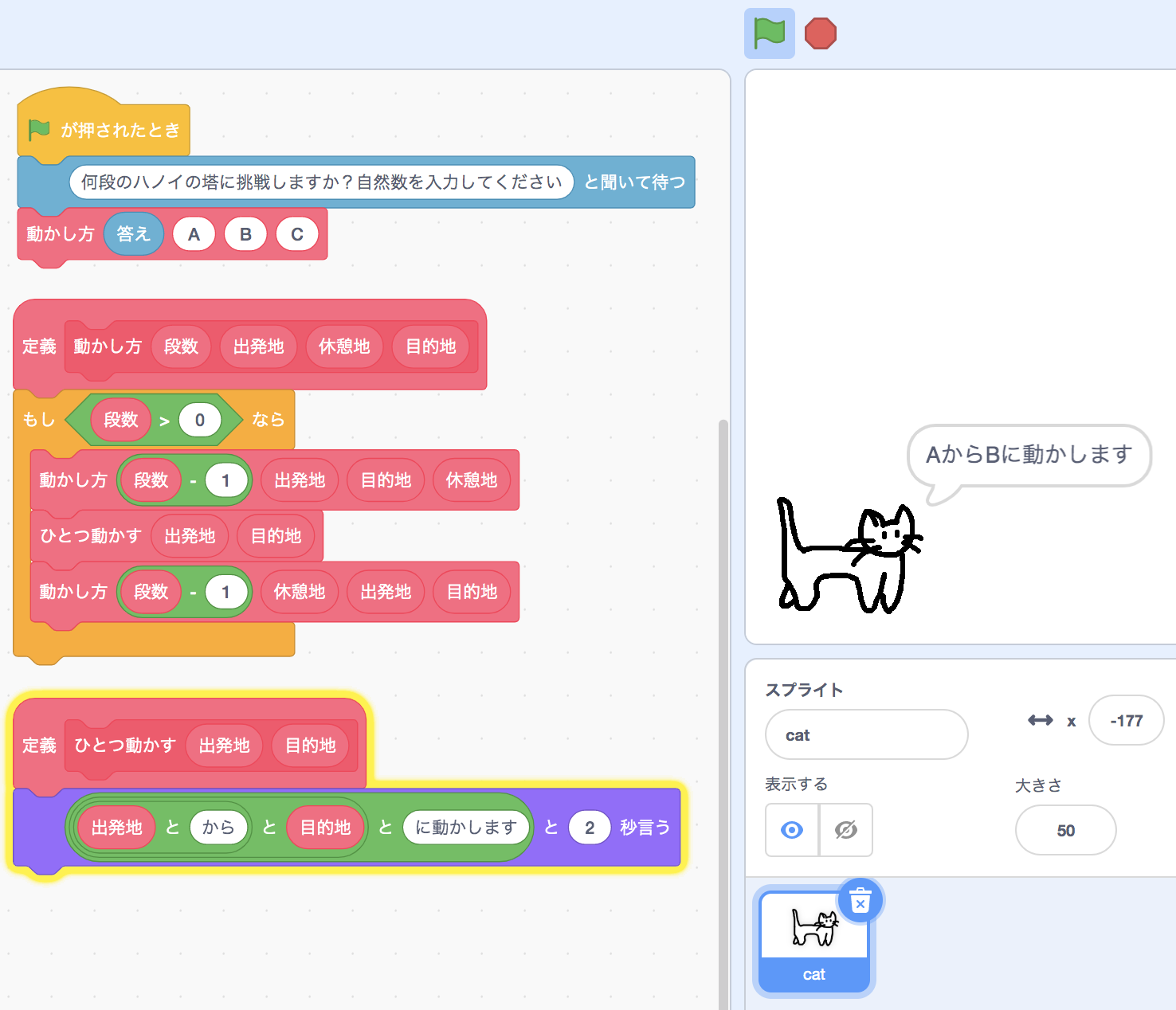
Scratch（スクラッチ）でハノイの塔を解くプログラム

出力はスプライトに2秒かけて動かす手順を言わせる方法にしました。4段のハノイの塔の場合、出力内容は次のようになります。

  • AからBに動かします
  • AからCに動かします
  • BからCに動かします
  • AからBに動かします
  • CからAに動かします
  • CからBに動かします
  • AからBに動かします
  • AからCに動かします
  • BからCに動かします
  • BからAに動かします
  • CからAに動かします
  • BからCに動かします
  • AからBに動かします
  • AからCに動かします
  • BからCに動かします

実際にコインなどで試していただくと、この手順で正しく4枚の円盤全てをAからCに動かすことができることを確認していただけると思います。 塔が何段あってもこの短いコードで正解の動かし方を得ることができる点が美しいですね。

# おまけ: C++でハノイの塔

ここで紹介したハノイの塔のScratchプログラムと同等の処理を行うC++のプログラムを掲載します。 眺めてみて「Scratchと同じだなぁ」と思っていただければオッケーです。

#include <iostream>

using namespace std;

void hanoi(int k, string from, string rest, string to) {
  if (k == 0) return;
  hanoi(k-1, from, to, rest);
  cout << from << "から" << to << "に動かします" << endl;
  hanoi(k-1, rest, from, to);
}

int main(void) {
  int N;
  cin >> N;
  hanoi(N, "A", "B", "C");
  return 0;
}

実行結果

$ echo 4 | ./a.out 
AからBに動かします
AからCに動かします
BからCに動かします
AからBに動かします
CからAに動かします
CからBに動かします
AからBに動かします
AからCに動かします
BからCに動かします
BからAに動かします
CからAに動かします
BからCに動かします
AからBに動かします
AからCに動かします
BからCに動かします

←