# 例題: ペンで図形を描画する
ペンで図形を描くプログラムは「タートルグラフィックス」という名前で昔から広く知られています。 プログラムの「順次、反復、条件分岐」という基本的な制御構造を視覚的に確認することができ、教育的だと思います。
Scratch(スクラッチ)でペンを使うにはペン拡張機能を有効化する必要があります。 プログラムを書く画面の左下に「ブロックに+マークが付いているボタン」があるのでこれをクリックして拡張機能を選ぶ画面に進み、「ペン(スプライトで絵を描く)」をクリックすればオッケーです。
# 正多角形の描画
まず正三角形を描いてみましょう。正三角形は「100歩進んで、120度左を向く」という操作を3回繰り返すと描画することができます。
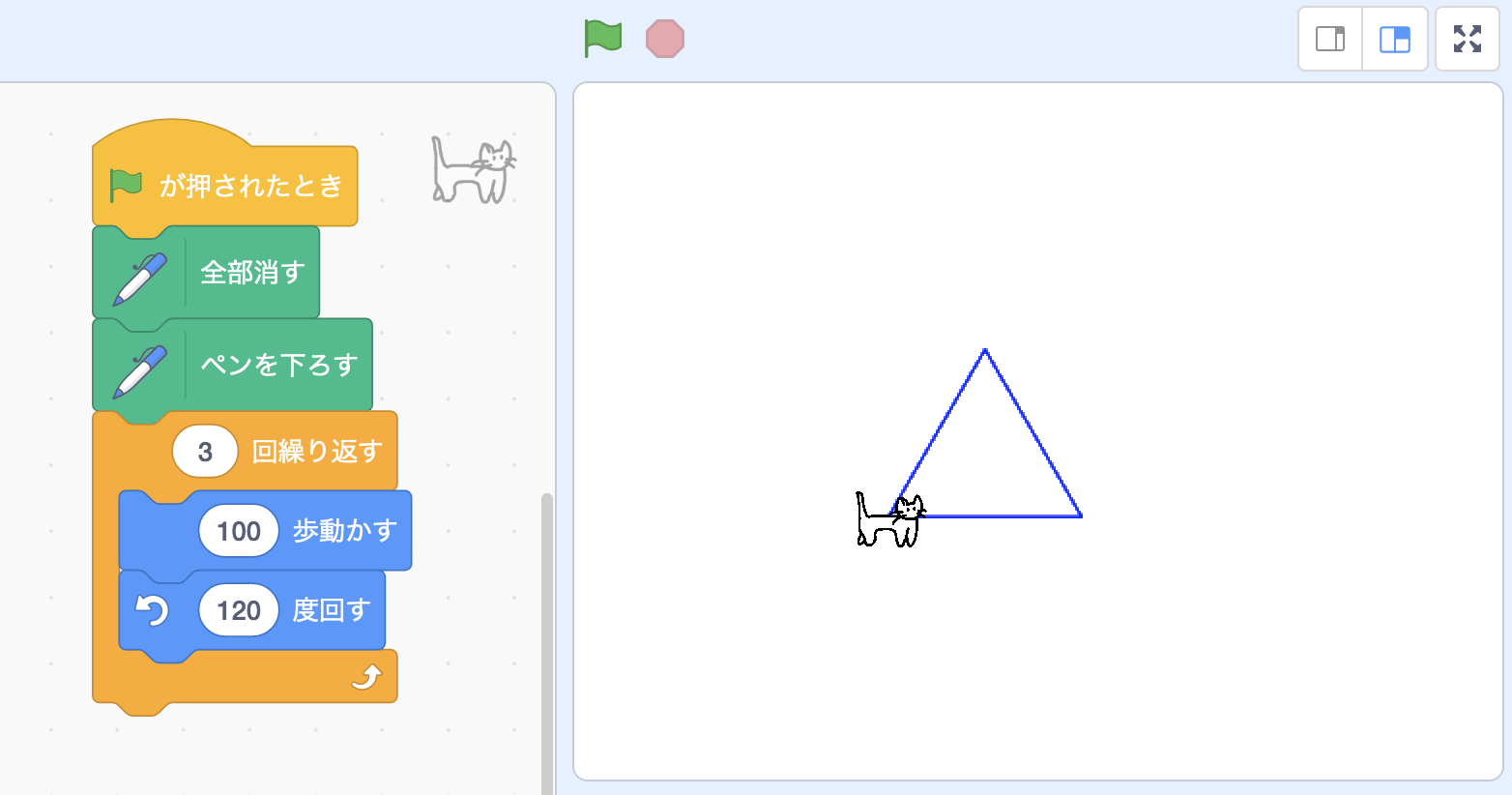
次は正方形。「100歩進んで、90度左を向く」という操作を4回繰り返すと描画することができます。
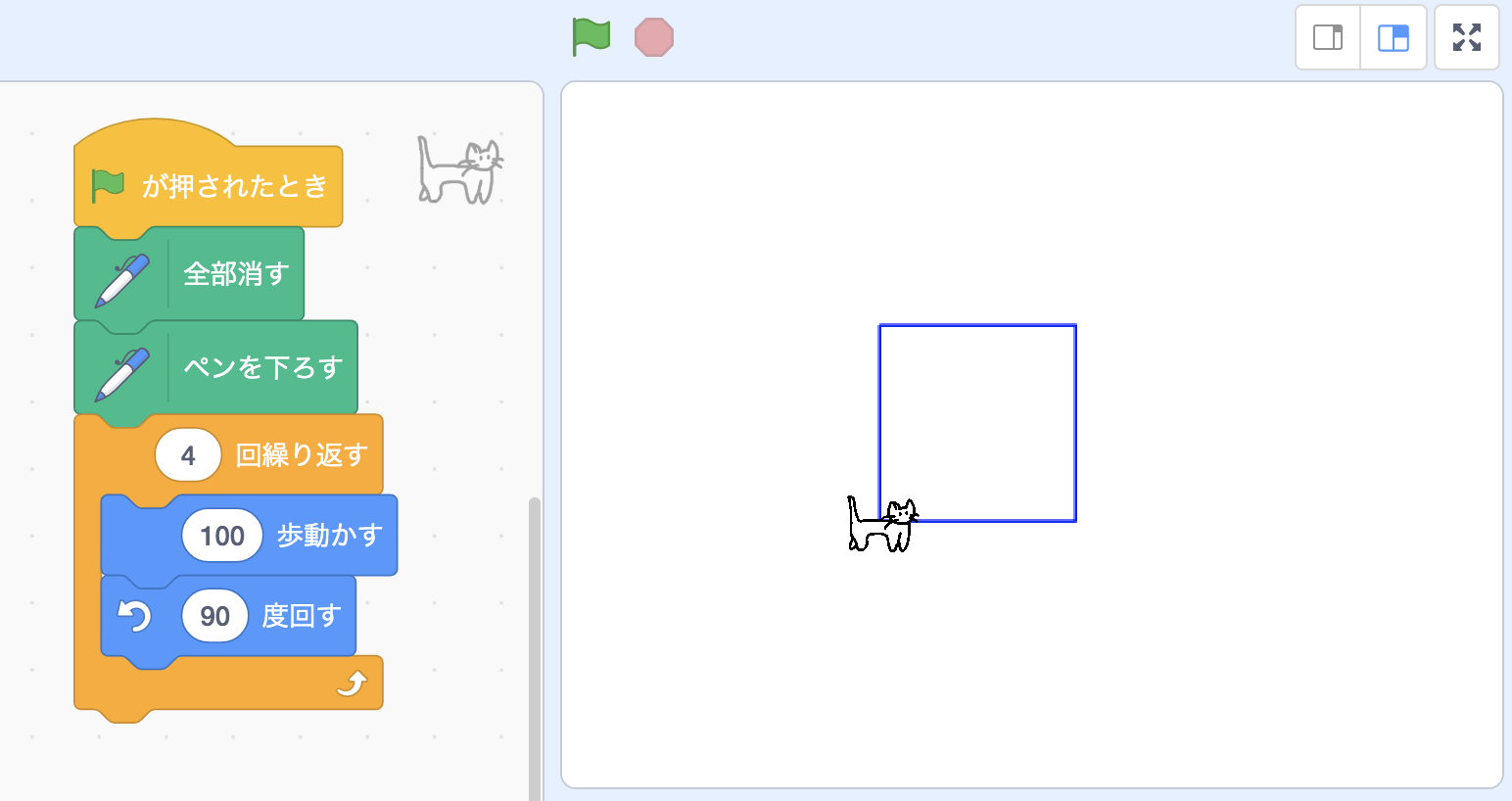
次は五角形。「100歩進んで、72度左を向く」という操作を5回繰り返すと描画することができます。
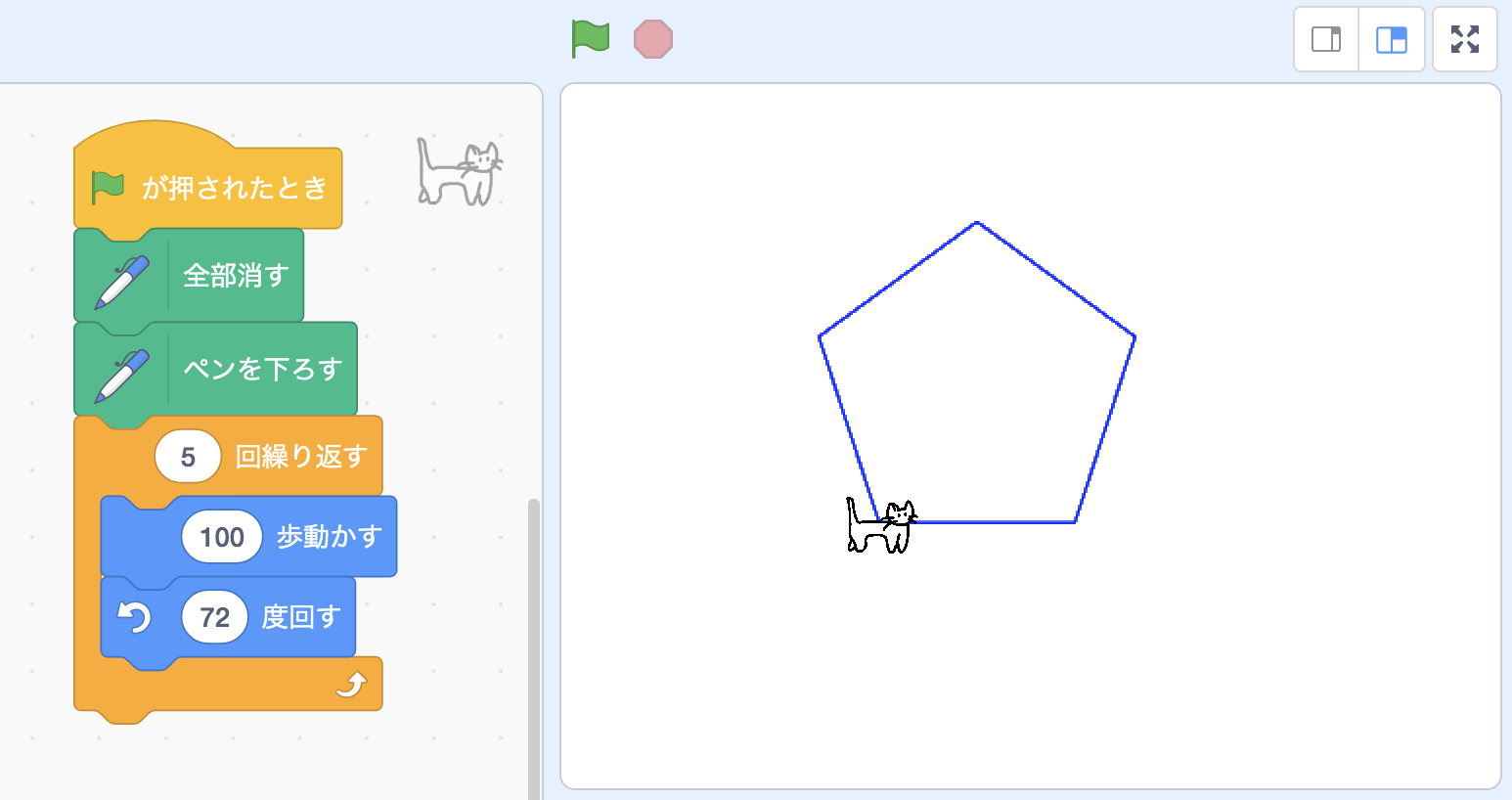
繰り返す回数と角度が図形ごとに違いますが、ここに法則があります。 正N角形を描画するとき、繰り返しはN回で、変える角度は正N角形の外角の角度、つまり「360÷N」度です。 これを利用すればN(辺の数)を入力するだけでどんな正多角形でも描画することができます。 次のプログラムは、その方法で描いた正六角形です。
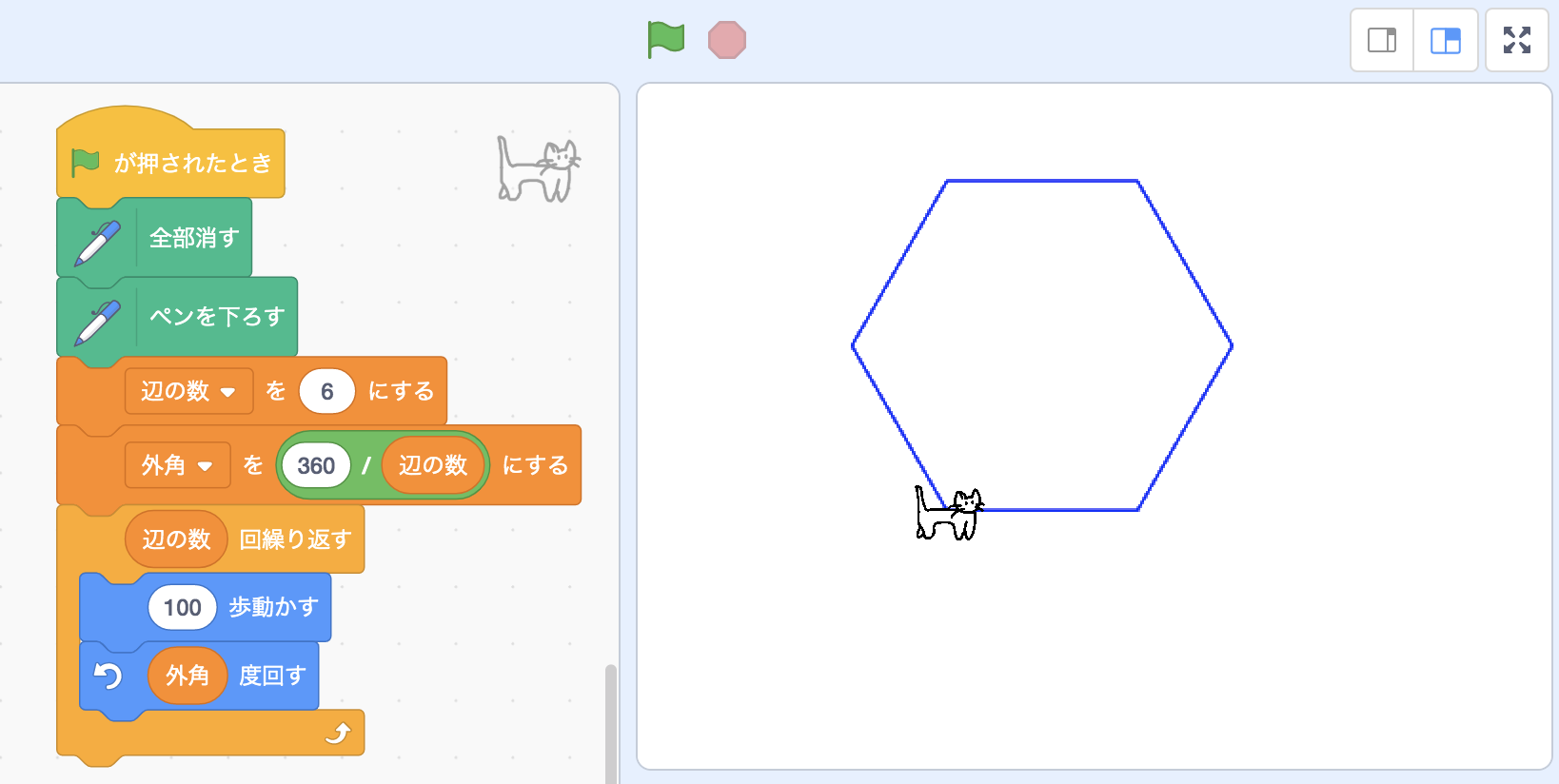
# 星形の描画
次に星形を描いてみましょう。
星形の描画には実は楽な方法があります。正多角形が「好きな回数、進んで曲がるを繰り返しながら、円周上を1周する」のに対して、星形は「奇数回、進んで曲がるを繰り返しながら、円周上を2周する」という操作を行っています。 つまり外角を求めるときの分母を1周分の360度から、2周分の720度に変えればオッケーです。
これは5つの辺からなる星形。
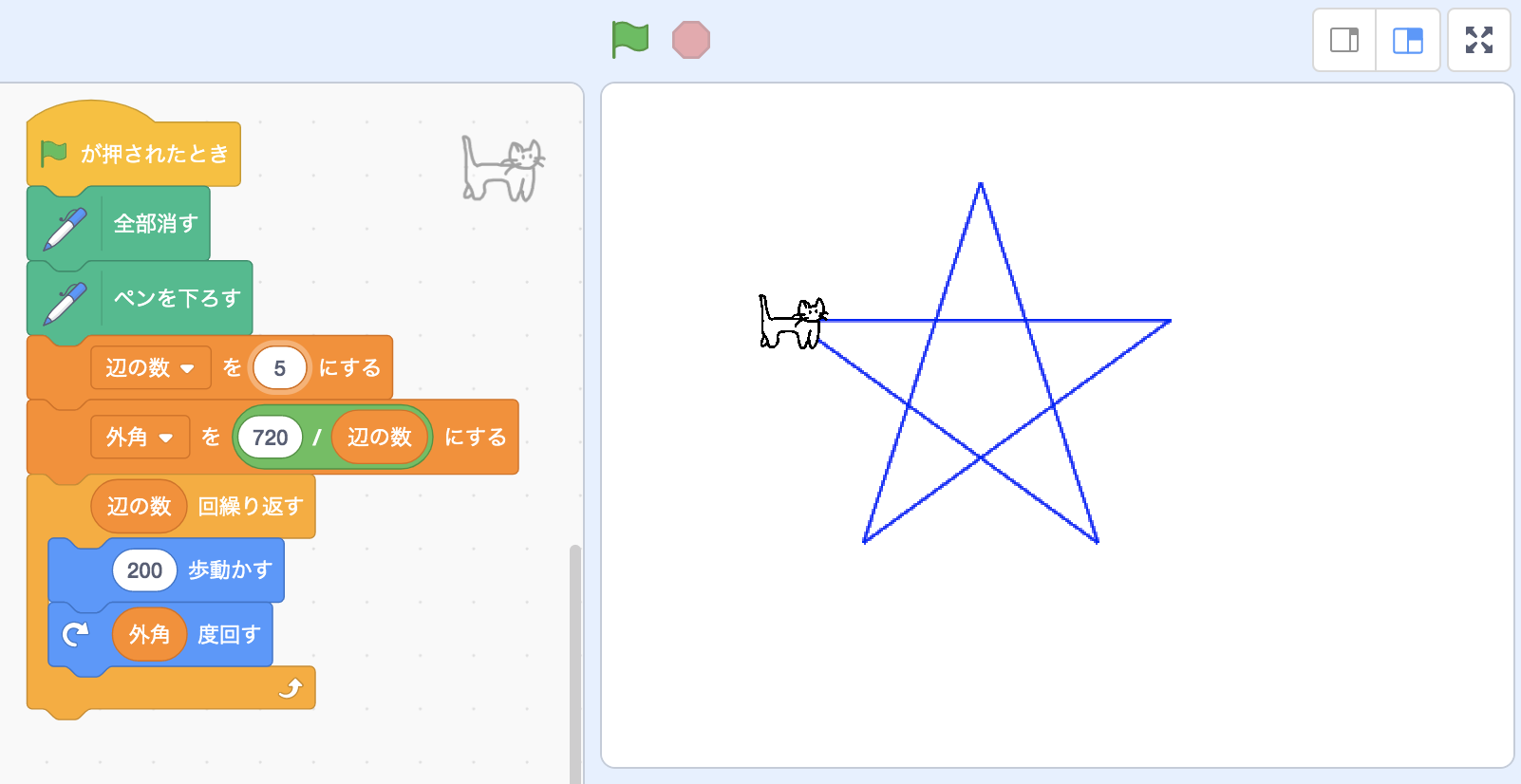
辺の数を7とかにしても、やや見慣れない形ですが星形のような図形になります。
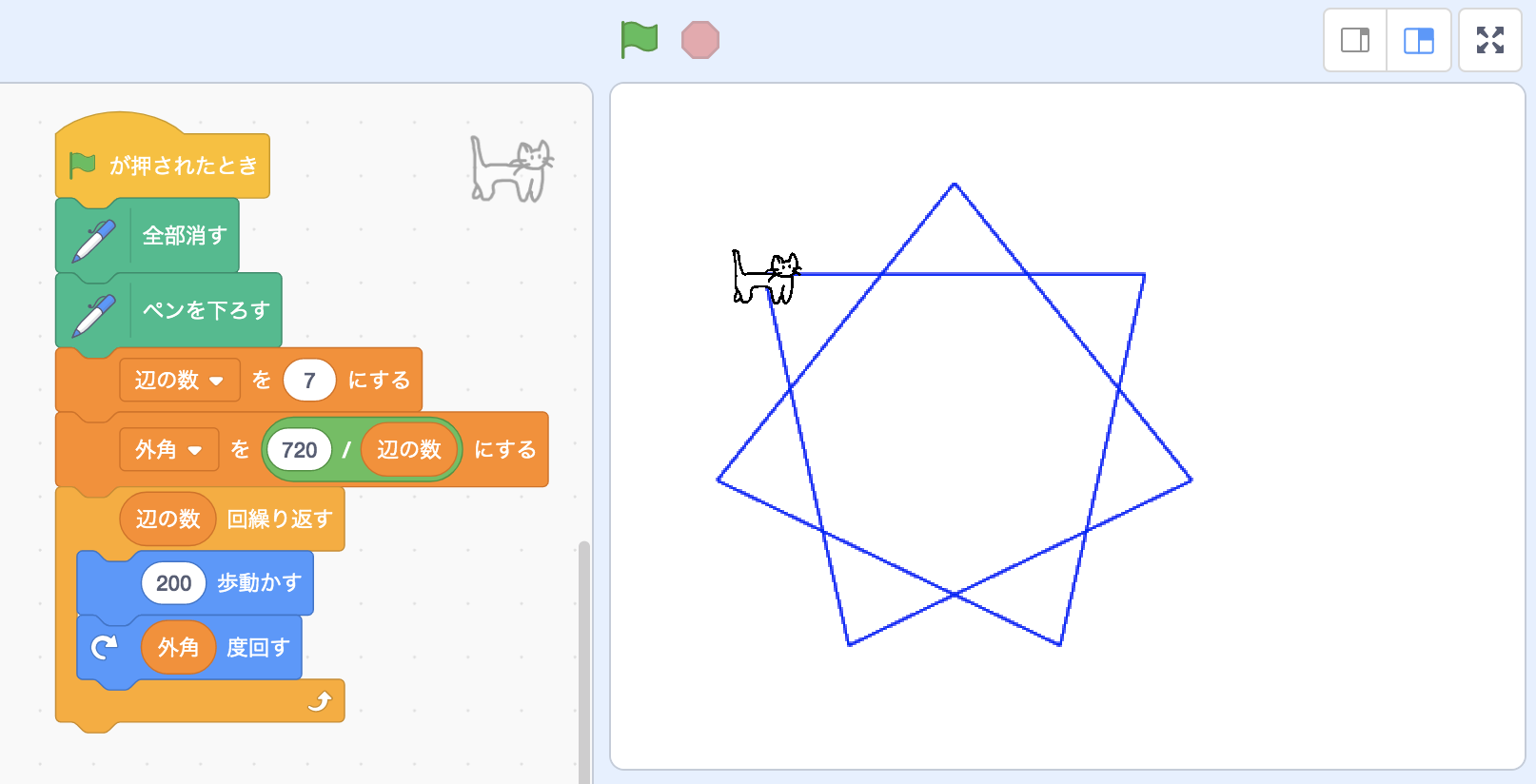
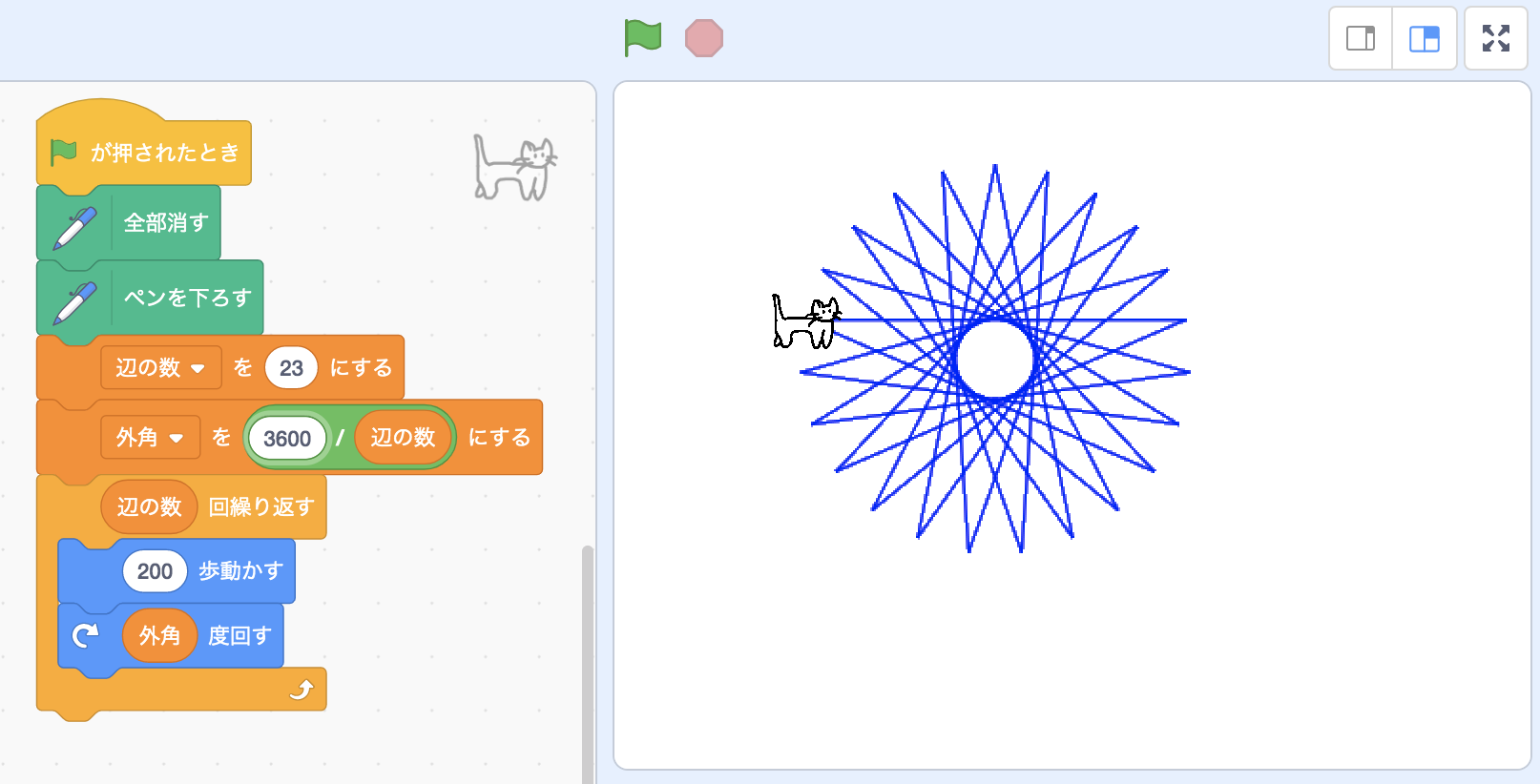
ちなみに辺の数と周回回数を適当に決めてもきれいな図形になります。 次のコードは「23回、進んで曲がるを繰り返しながら、円周上を10周する」というコードですが、なかなか装飾的な図形が得られました。 動かしてみると意外に美しい結果が得られることがあるというのはタートルグラフィックスの魅力的なところだと思います。
# フラクタル図形の描画
発展的な内容として、タートルグラフィックスによるフラクタル図形の描画を紹介します。
フラクタル図形とは図形の一部が全体と相似となっている図形のことです。 タートルグラフィックスでフラクタル図形を描くと、プログラミングの「関数の再帰的呼び出し」の視覚的なイメージが得られるので、教育的に良いです。
ここまでで紹介した正多角形や星形は「プログラマが書いた通りの図形が描画できた」程度の感触なんですが、フラクタル図形は「プログラマが書いたコード量をはるかに超える複雑な図形がコンピュータによって描画される魔法」のように感じられて惹き込まれると思います。
この節のコードはScratch(スクラッチ)のプロジェクトを共有するので、よかったら動かしてみてください。
# コッホ曲線を使った雪の結晶のような図形
プロジェクト共有: コッホ曲線を使った雪の結晶のような図形の描画
コッホ曲線とは、直線を繰り返し尖らせていくことで得られる図形です。(下図の画像: Wikipedia:コッホ曲線より引用 / Kkairri (original made by Solkoll~commonswiki) [Public domain])
このコッホ曲線を3つ繋げると雪の結晶のように見えて美しいです。
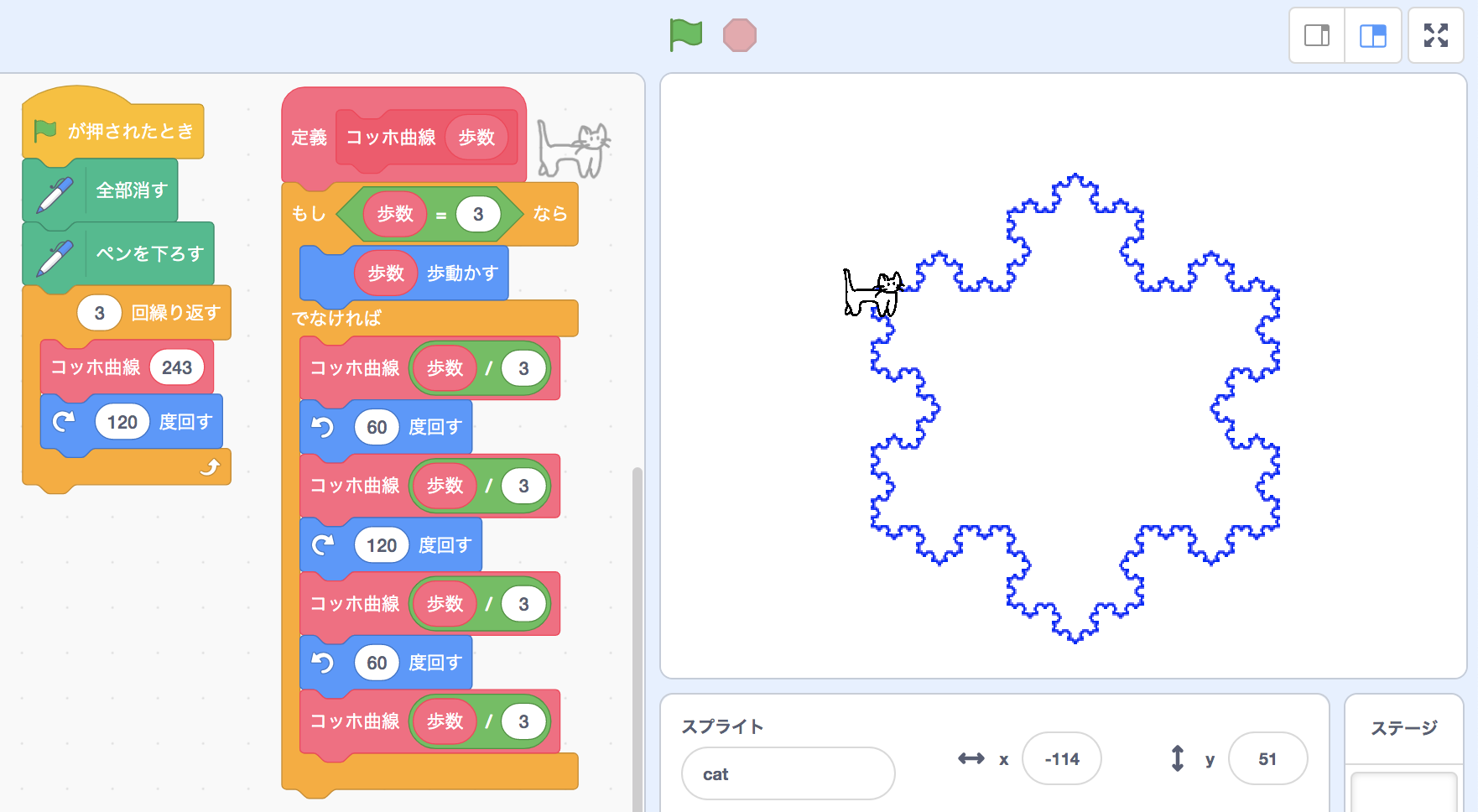
Scratch(スクラッチ)のプログラミングでは、「コッホ曲線的な移動方法」というものを再帰的にブロック定義すると描画することができます。
「N歩のコッホ曲線的移動1回」は、「歩数がN/3の小さなコッホ曲線的移動4回」から構成されます。 さらにこれは「歩数がN/9のより小さなコッホ曲線的移動16回」から構成され、さらにこれは「歩数がN/27のもっと小さなコッホ曲線的移動64回」から構成され……と続いていくのですが、この部分はコンピュータが定義に従って実行してくれます(便利)。
数学的には再帰が無限に続くのが正しいのですが、プログラミングでこれをすると処理が終わらないので適当なところで打ち切る必要があり、上の図のコードでは「歩数が3のときは再帰せずただまっすぐ進むだけ」としています。
# ドラゴン曲線
プロジェクト共有: ドラゴン曲線
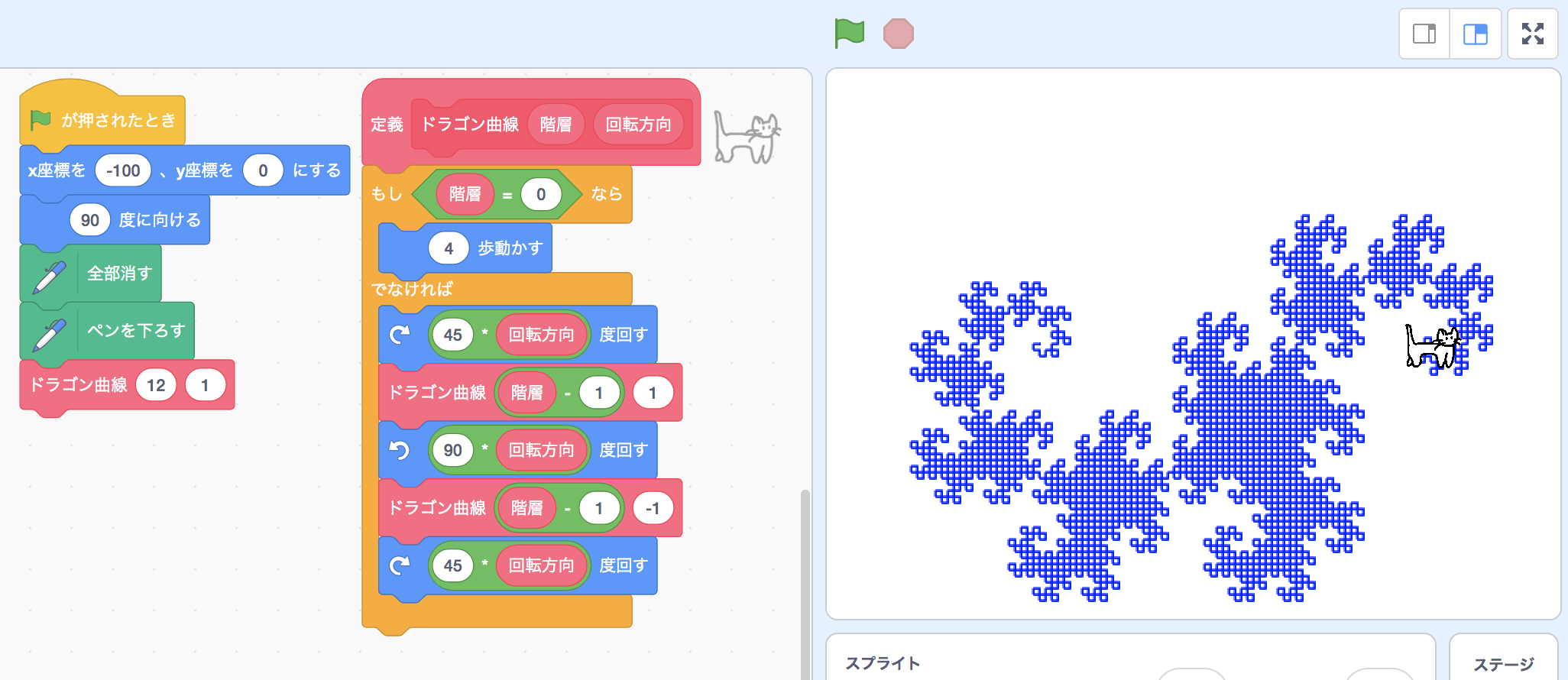
名前がカッコイイ! 詳細はWikipedia:ドラゴン曲線をご覧ください。 再帰の中で向きを変える方向が逆になっているところがあって少しややこしいですが、ブロック定義の引数に回転方向をもたせる工夫をするとスマートに実装できます。
# シェルピンスキーの三角形(シェルピンスキーのギャスケット)
プロジェクト共有: シェルピンスキーの三角形
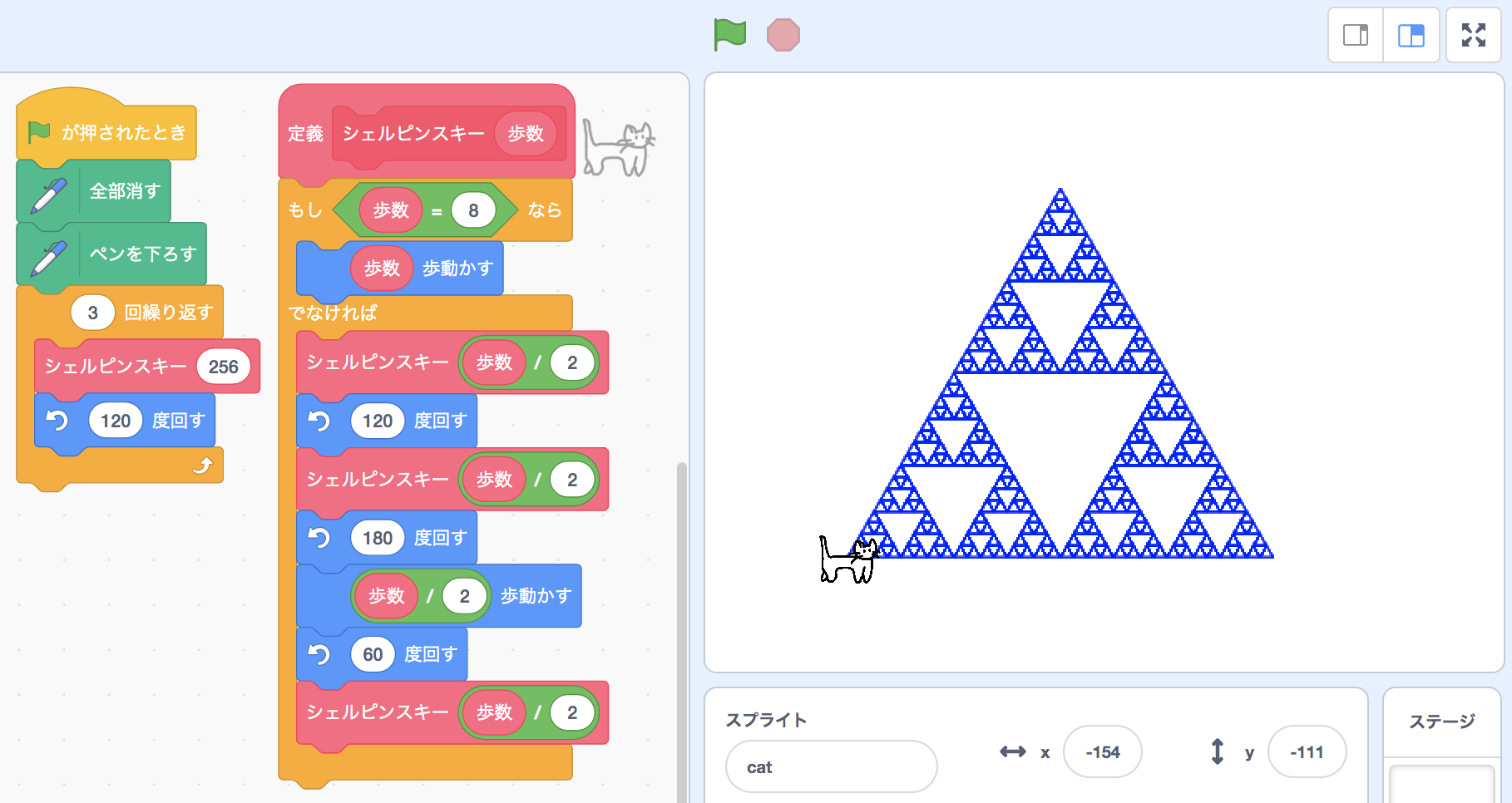
これはシェルピンスキーの三角形というフラクタル図形です。 数学者ヴァツワフ・シェルピンスキにちなんで名付けられました。 正三角形の真ん中をくり抜く、という操作を再帰的に行うことで得られる図形です。 詳細はWikipedia:シェルピンスキーのギャスケットをご覧ください。
