例題: 素数判定

Scratchで素数かどうか調べる方法、および素数判定のアルゴリズムの高速化について解説します。

素数判定

プログラムの入出力部分は、スプライトが入力値を受け取り、これが素数かどうか判定して「素数です」または「素数ではありません」と答えるという風にします。

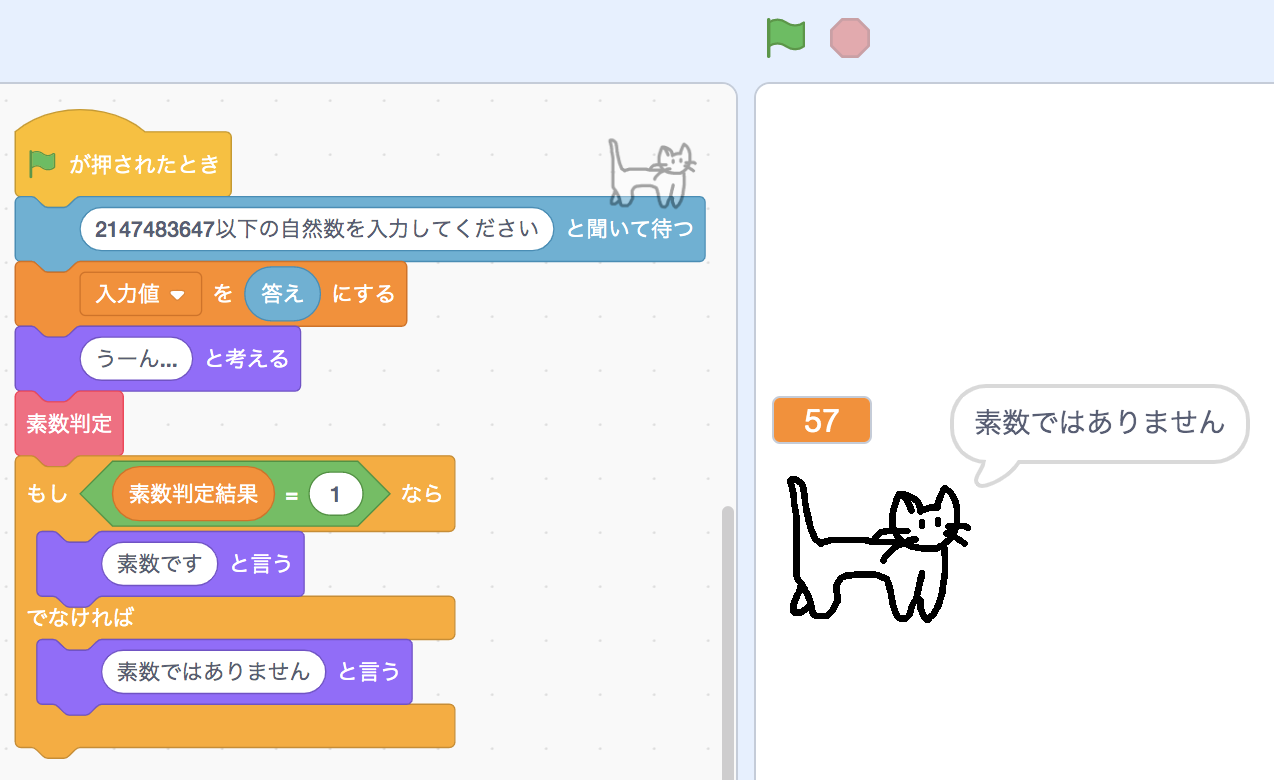
Scratchはプログラミング言語の制約として正確に表せる整数の精度に限界があり、2147483647（4バイト整数の最大値）を超えると値がズレる可能性があるので、念のため入力時に但し書きしてあります。

次に、素数判定の中身を作っていきます。

素数とは「1より大きい自然数で、正の約数が1と自分自身のみであるもの」のことなので、次のように処理すれば判定することができます。

• 入力値が2未満なら素数ではない
• 変数「割る数」を2以上、入力値未満の範囲で動かし、入力値が割り切れれば素数ではない

今回は下図のように実装してみました。

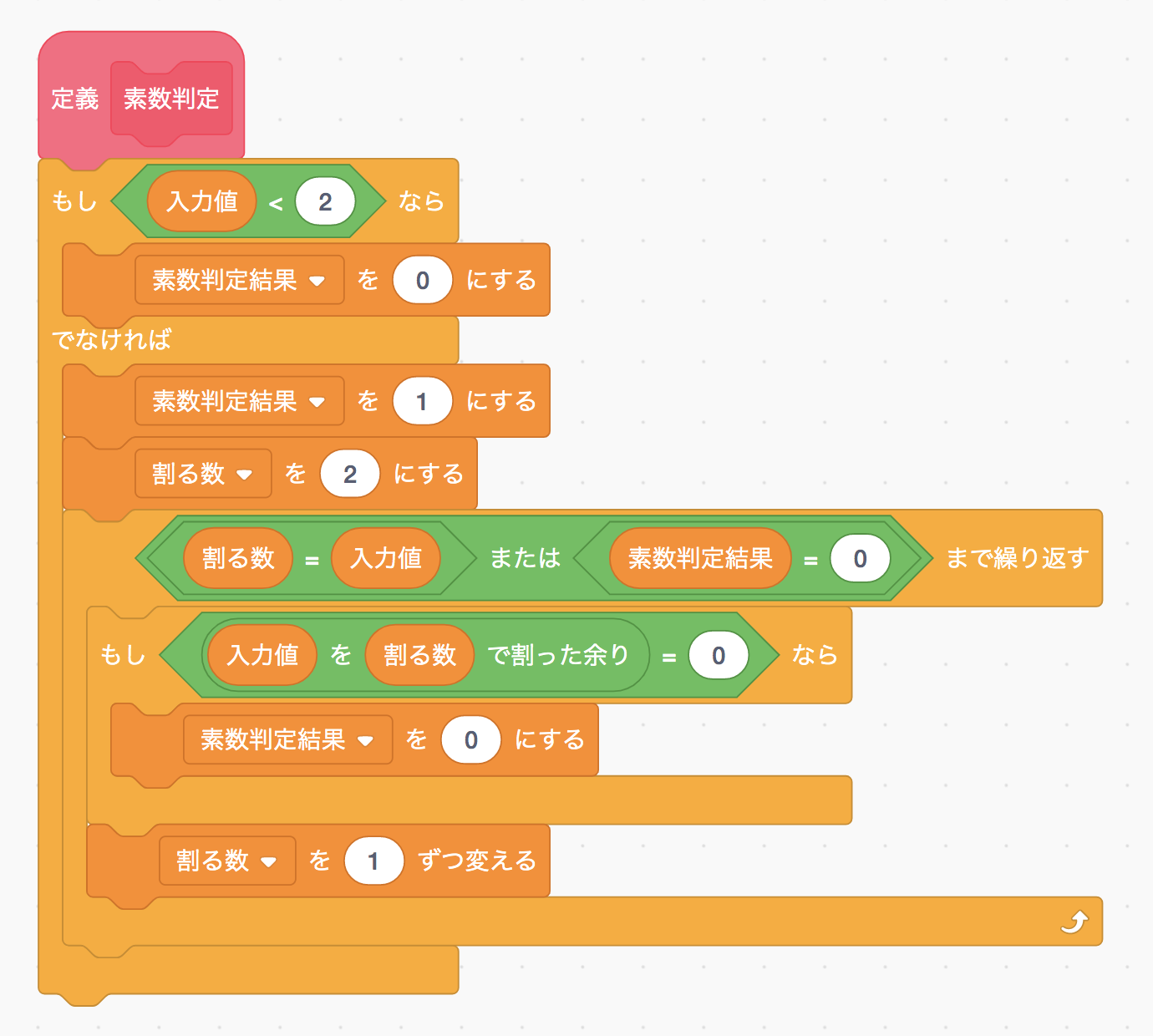
判定結果は変数「素数判定結果」に格納することにし、素数のとき1、素数でないときに0となるようにしています。

割り切れるかどうかのテスト部分は、「割る数」をまず2にセットし、これを1ずつ増やしながら割り切れるかどうかをチェックし、入力値と等しくなったタイミングで繰り返しから抜けます。 ここで、一つでも割り切れる数が見つかればそれ以上はチェックする必要がないため、繰り返しを抜ける条件として「素数判定結果が0であること」（割り切れる数が見つかったこと）を追加しています。

素数判定の速度改善

「10000019」は素数でしょうか？

ここまでで作成したプログラムで実験してみると、45秒後に「素数です」と答えてくれました。 つまり素数判定に45秒かかっていることになります。 もうちょっと速くしたいですね。

割り切れるかどうかのチェックに偶数を入れているのが無駄でしょうか。 2で割り切れなかった場合、もう偶数で割り切れないことは確定しているので、それ以降のステップでは3以上の奇数のみ試せば良いことが分かります。 これだとチェック数が半分になるので2倍高速化します。 こういった改善は「定数倍高速化」と呼ばれています（たぶん通称）。 しかし定数倍高速化はアルゴリズムの勉強の際にはあんまり重要視されません。

もっと劇的に速くする方法があります。 入力値をNとしたとき、実は√Nより大きい数については割り切れるかどうかのチェックを行う必要がありません。

• Nを割り切る√N以上の整数Aが存在すると仮定する
• N÷Aを整数Bとして、整数BもNを割り切ることができる
• このとき整数Bは√N以下である（整数Bが√Nより大きいとすれば、A×BはNより大きい値となってしまうので矛盾）

このことから、√Nまで試せば整数Bの方で割り切れるかどうかチェック済みなので、√Nを超える分はチェックする必要がないのです。 これにより素数判定部分の計算量を O(N) から O(√N) に改善することができます。

10000019の素数判定でいうと、改善前のアルゴリズムでは「2〜10000018」の範囲の整数で割り切れるかどうかチェックしていたのですが、√10000019=3162.28...なので「2〜3162」の範囲だけ試せば実は十分ということで、3000倍くらい高速化することができます。 45秒の3000分の1なので0.015秒くらい。 一瞬ですね。

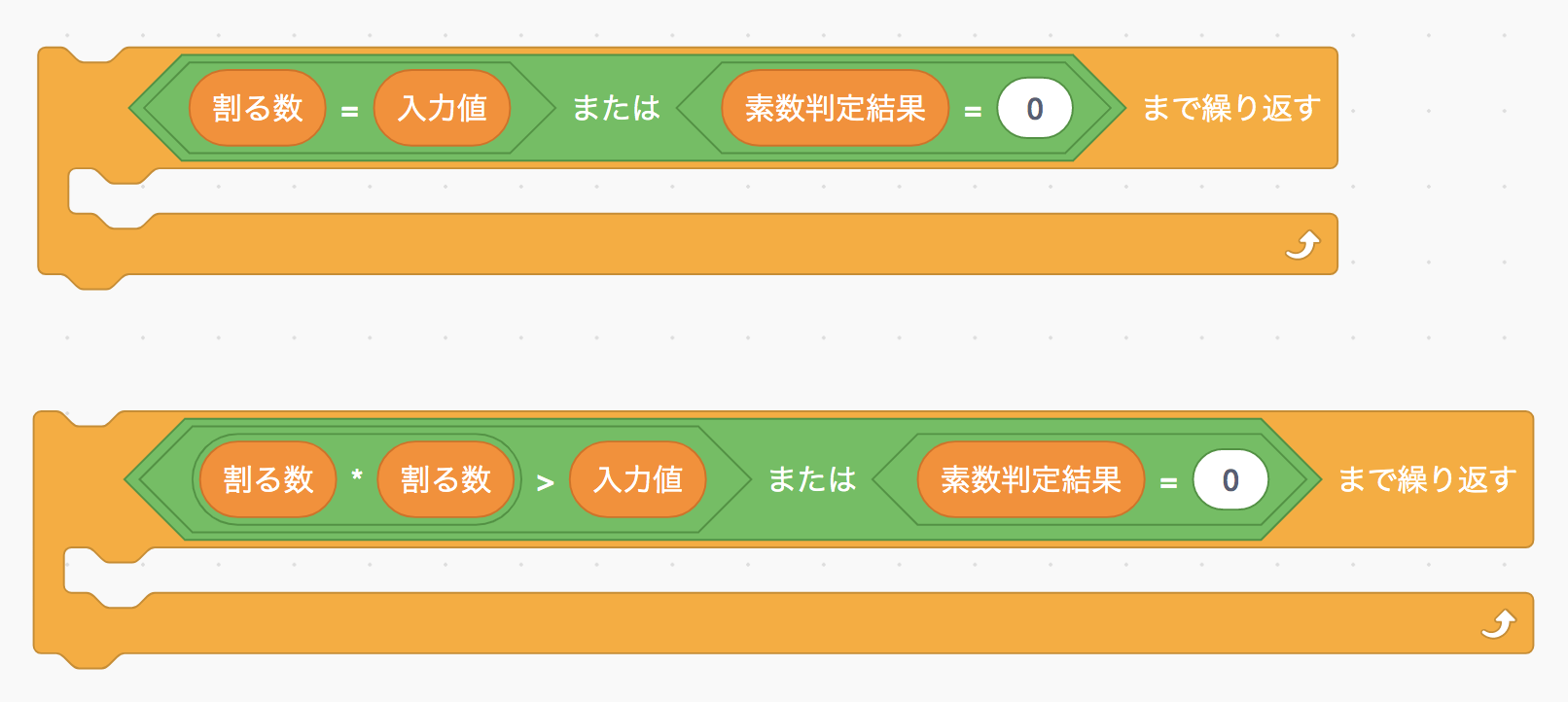
改善後のScratchプログラムは下のようになります。

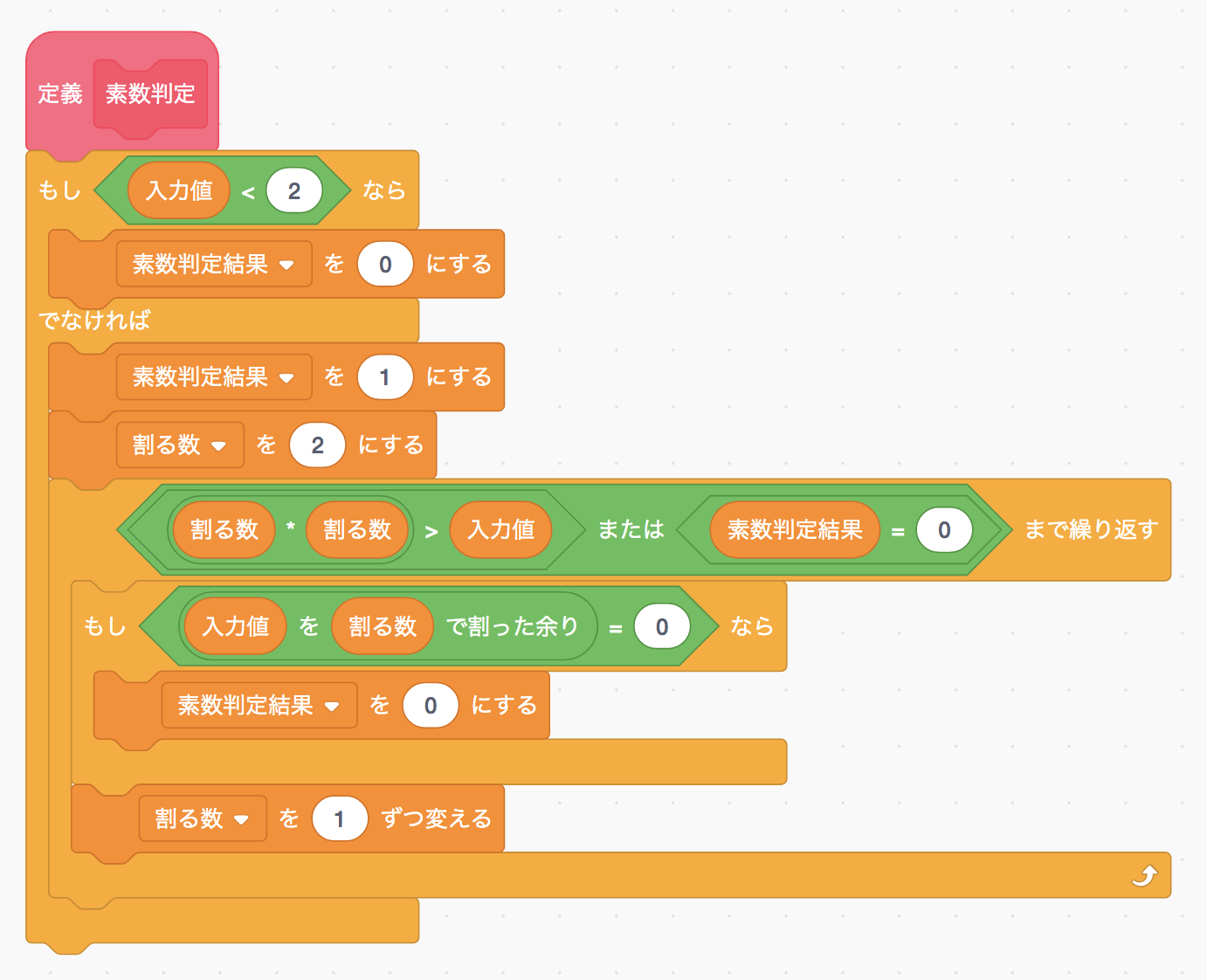
差分は一箇所しかなくて、割り切れるかどうかのチェックの繰り返しを抜ける条件の一部が「割る数 = 入力値」から「割る数 * 割る数 > 入力値」に変わっているだけです。

このように論理的な考察とちょっとしたコードの違いでプログラムの性能が劇的に改善することは実務でもたまにあり、これがプログラミングに面白さ（そして悲しさ）を与えています。 こういうのが好きな方は、アルゴリズム的なスキルのみを競う「競技プログラミング」というのがあるので調べてみてください。

高速化後の素数判定のScratchプロジェクトを共有します→素数判定

おまけ: C++で素数判定

ここで紹介した素数判定のScratchプログラムと同等の処理を行うC++のプログラムを掲載します。 眺めてみて「Scratchと同じだなぁ」と思っていただければオッケーです…が、今回はあんまり同じじゃないかも。 C++の方が関数が値を返すという性質を使ってスッキリと実装できます。

#include <iostream>

using namespace std;

// 素数かどうかを真偽値で返す関数
bool is_prime(int n) {
  if (n < 2) {
    return false;
  }
  for (int i = 2; i * i <= n; i++) {
    if (n % i == 0) {
      return false;
    }
  }
  return true;
}

int main(void) {
  int input;
  cin >> input;
  if (is_prime(input)) {
    cout << "素数です" << endl;
  } else {
    cout << "素数ではありません" << endl;
  }
  return 0;
}

実行結果

$ echo 57 | ./a.out
素数ではありません

$ echo 10000019 | ./a.out 
素数です