プログラミング教育のためのスクラッチ例題集

# 例題: 素因数分解

Scratchで入力された値を素因数分解するプログラムについて解説します。

基本的な部分は素数判定と似ていますが、素数判定では割り切る数を一つ見つければそれで良かったのに対し、素因数分解では割り切る素数とその回数を全て見つける必要があり、ちょっと複雑になります。

Scratchプロジェクトを共有しています: 素因数分解

# 入出力部分

入力はスプライトの「聞いて待つ」で答えを受け取り、出力は素因数分解の結果をリストに入れて表示する形式にします。

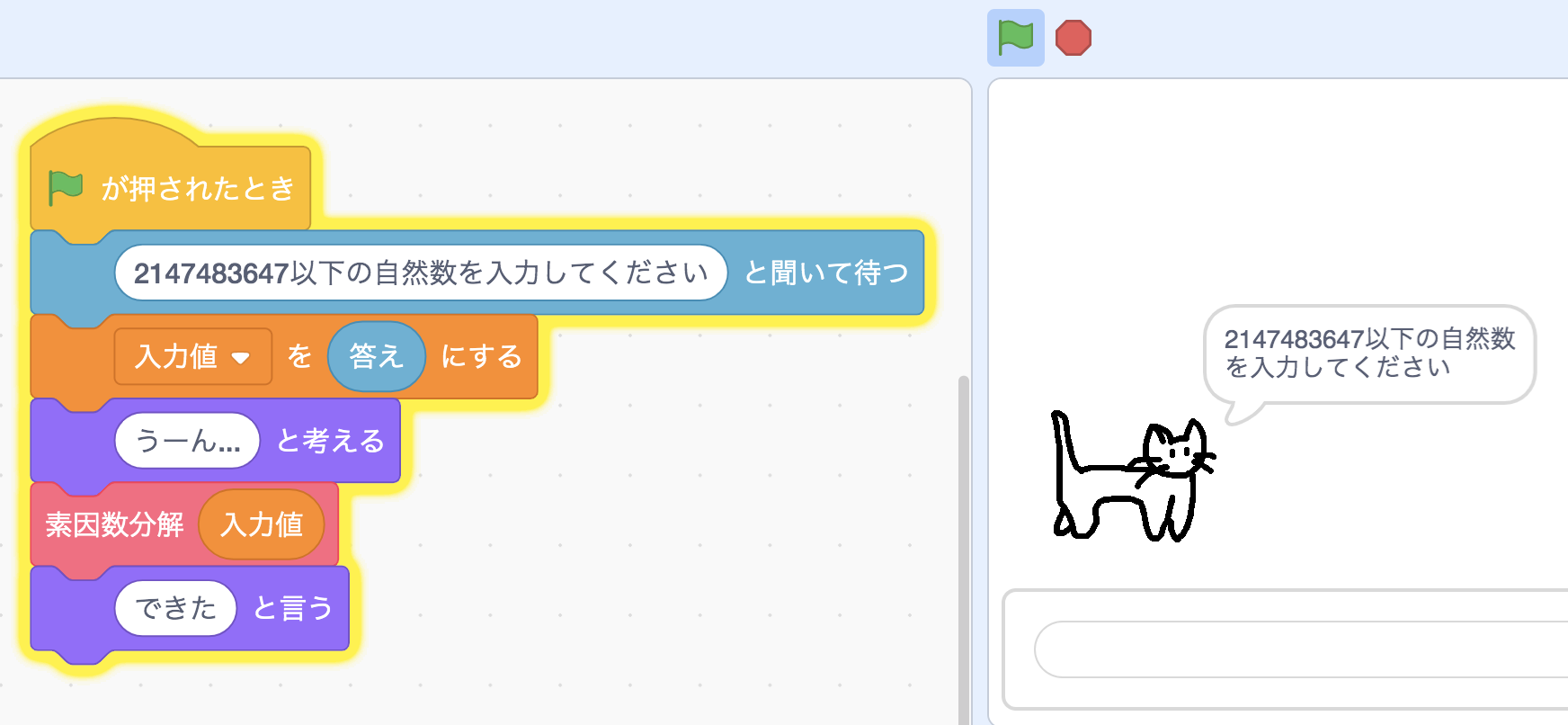
Scratchで素因数分解 入力と出力

Scratchはプログラミング言語の制約として正確に表せる整数の精度に限界があり、2147483647（4バイト整数の最大値）を超えると値がズレる可能性があるので、念のため入力時に但し書きしてあります。

# 数学的な考察

割り切れる数を総当りする方法で素因数分解をしようと思うのですが、そのままやると自然数Nについて2〜Nの範囲で総当りすることになり、計算量がO(N)となって時間がかかります。

ここでプログラムの高速化のためにちょっと数学的な考察をします（算数の範囲の話なので難しくはないです）。

自然数Nを√Nより大きい素数で2回以上割り切ることはできません。

Nが√Nより大きい素数で2回以上割り切れると仮定すると、√Nより大きい2つの素数p,qのうち（p=qでもよい）、Nがp×qの倍数になるものが存在するということになりますが、p×qはNより大きい値なので、Nがp×qの倍数となることは有り得ず、矛盾します。

（ここでは自然数は1以上の整数のことです。ゼロを自然数に含めることもあるので念のため。）

よって自然数Nの、√Nより大きい素因数は高々1つ（0個か1個）存在します。 かつ存在した場合、その次数は1です。

というわけで、Nの素因数の候補として2〜√Nの範囲で総当りし、最後に割り切れないものが残っていればそれが√Nより大きい高々1つ存在する素因数である、という方法で正しく素因数分解できることが分かります。 このアルゴリズムの計算量はO(√N)で、比較的高速に動作します。

# 素因数分解の実装

Scratchで素因数分解するプログラムを次のように作成しました。

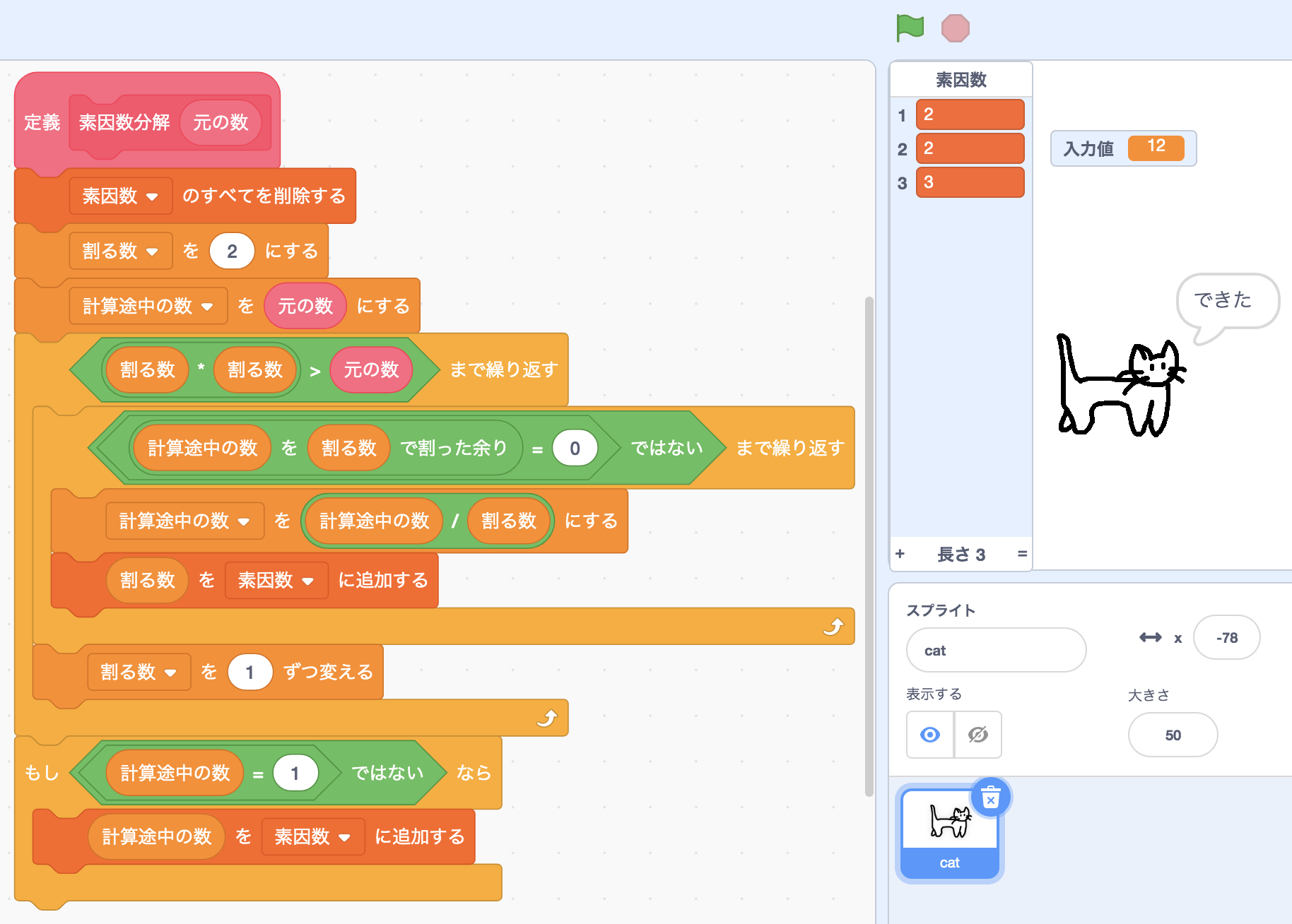
Scratchで素因数分解を行うプログラム

  • 「計算途中の数」としてNをコピーする
  • 「割る数」を2から√Nの範囲で1ずつ変えながら、次の操作を繰り返す
    • 「計算途中の数」が「割る数」で割り切れなくなるまで、次の操作を繰り返す
      • 「割る数」を素因数リストに追加する
      • 「計算途中の数」を「割る数」で割った値で置き換える
  • 最後にもし「計算途中の数」が1ではない場合は、√Nより大きい素因数が存在したケースなので、これを素因数リストに追加する

ここで作ったプログラムは繰り返しの中に繰り返しがある構造（いわゆる二重ループ）を持っています。

割り切れるかどうかのチェックで、「割る数」のほうが素数でないことがあり、これでは素因数分解にならないじゃないかと思った方もいらっしゃるかと思いますが、「割る数」として小さい数から総当りしているので、「計算途中の数」が素数でない数で割り切れることは無いです。 例えば「元の数」が1000で「割る数」が10の時、「計算途中の数」は2と5で割り切れるだけ割り切られ済みで、10ではもう割り切れません。

内側の「計算途中の数が割る数で割り切れなくなるまで…」の中身が1度も実行されないまま次の外側の繰り返しに移ることが多いですが、これで正しく動きます。

# おまけ: C++で素因数分解

ここで紹介した素因数分解のScratchプログラムと同等の処理を行うC++のプログラムを掲載します。 眺めてみて「Scratchと同じだなぁ」と思っていただければオッケーです。

#include <iostream>
#include <vector>

using namespace std;

vector<int> prime_factorization(int n) {
  vector<int> result;
  int tmp = n;
  for (int i = 2; i * i <= n; i++) {
    while (tmp % i == 0) {
      result.push_back(i);
      tmp = tmp / i;
    }
  }
  if (tmp != 1) {
    result.push_back(tmp);
  }
  return result;
}

int main(void) {
  int n;
  cin >> n;
  vector<int> result = prime_factorization(n);
  for (int i = 0; i < result.size(); i++) {
    cout << result[i] << endl;
  }
  return 0;
}

実行結果

$ echo 12 | ./a.out  
2
2
3

← 例題: ハノイの塔 →